FDTD法による電磁波解析
FDTD法とは
FDTD法とは、以下の(1)式で表されるMaxwell方程式を時間的(Time)、空間的(Domain)に離散化し陽的な時間進行法を用いて経時的な電磁界強度を求める手法です。
ここで、電界:
(1)
これから、FDTD法について具体的に分かりやすく説明します。
なお、電流密度は
*FDTD法とは、Finite-Difference Time-Domain methodの略号です。
Keyword:FDTD,FDTD法,電界,磁界,電束密度,磁束密度,Maxwell方程式,FDTD method,Finite-Difference,Time-Domain method,electromagnetic field,Maxwell equation
What is FDTD?
FDTD method for an electromagnetic field is a numerical scheme to obtain the time domain distribution of electromagnetic field by solving the explicitly discretized Maxwell’s equations which are represented by the following equations (1). Here, we define an electric field as
(FDTD method is an abbreviation for Finite-Difference Time-Domain method)
格子は多くの場合、図1のような電界及び磁界ベクトルの配置が半格子ずれたスタガード格子(Staggered Grid)を用います。FDTD法では電磁波の波形を再現するために格子は解析対象とする波長よりも十分に小さい必要があります。かつ時間的な陽的解法ですので、時間進行法に用いるタイムステップは格子幅
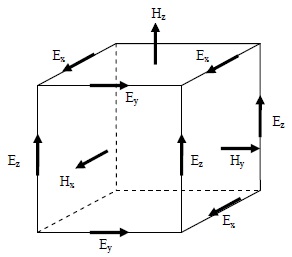

図1 スタガード格子
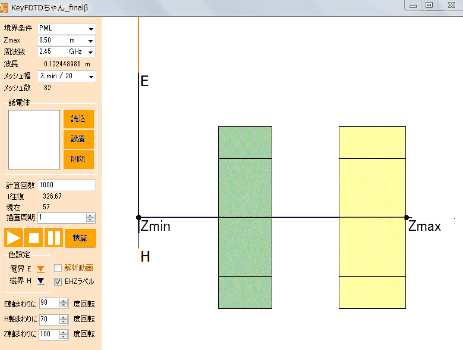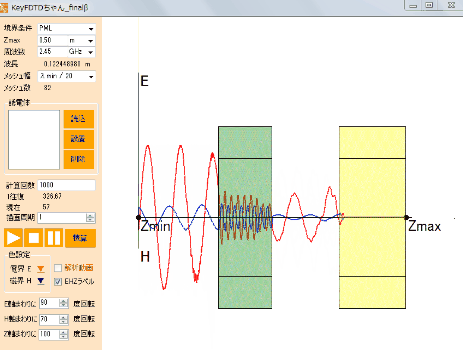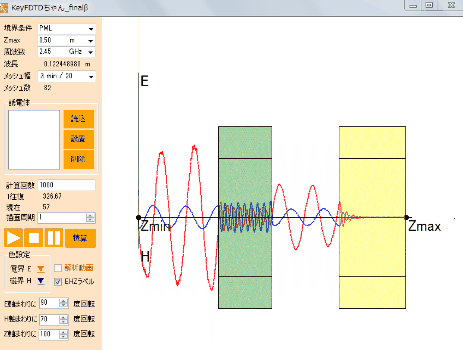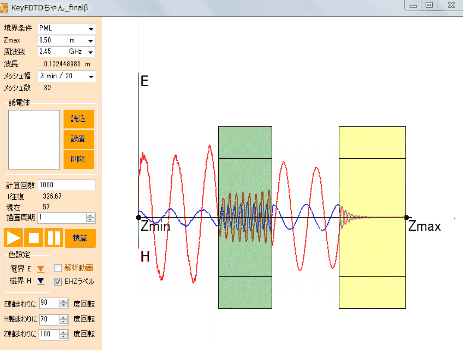
可視光(波長400nm~800nm程度)を扱う場合にはサブマイクロ~マイクロメートルの解析領域を対象とするような問題で非常に効率的な解析が可能です。特にナノスケールの構造をもった物体の電磁波の反射・散乱・透過特性の解析やプラズモン解析などでは多くの実績があります。また電子レンジのようなマイクロ波加熱問題も波長と解析領域の大きさが近い場合が多く効率よく解析ができます。さらに波長の長い電波は建物の壁面を考慮することはできませんが、建物を一つの物体と見立てれば大空間における解析も可能です。
お問い合わせ・資料ダウンロード・入門動画視聴のお申し込みはこちら
お問合せフォームを開く
FDTD法とは