白金ナノ粒子のFDTD法による光学特性シミュレーション
Abstract
電磁波解析ソフトKeyFDTDを使用して白金ナノ粒子層の光学特性を解析した。白金の物性値を分散モデルで近似し、粒径80nmの白金ナノ粒子層にガウシアンパルスを入射、可視光~紫外域の透過・反射スペクトルを算出した。白金ナノ粒子層は波長全体でほぼ反射は無いが、波長570[nm]以下で局在表面プラズモン共鳴により透過率が低下し、波長430[nm]で透過率の最小値を示した。
The optical characteristic of a layer of platinum nanoparticles were analyzed by using the electromagnetic wave analysis software KeyFDTD. The dielectric properties of platinum were approximated by a dispersion model, and a Gaussian pulse was incident into a layer of 80 nm platinum nanoparticles. And the transmission and reflection spectra in the visible to UV region were calculated. The platinum nanoparticle layer shows little reflection across all wavelengths, but the Local surface plasmon resonance reduces the transmission below wavelength 570 [nm] and shows the minimum transmission at wavelength 430 [nm].
1. 解析概要
本報告書では電磁波解析ソフトKeyFDTDを用いて白金ナノ粒子の光学特性をシミュレートした結果を報告する。
2. 解析条件
解析モデルをFig.1に示す。
 Fig.1 Simulation model
Fig.1 Simulation model
水中(n=1.33)に粒径80[nm]の白金ナノ粒子が周期的に整列した粒子層をシミュレーション対象とした。解析領域はx、y方向を320[nm]、z方向を520[nm]、メッシュ幅は2.5[nm]とした。境界条件はx、y方向が周期境界条件、z方向が吸収境界条件MUR1である。白金の複素誘電率は1つのDrudeモデルと3つのLorentzモデルの線形和でモデル化した(Eq.1)にTable.1、2のパラメータを設定して近似した。ここで右下添え字の数字は分散モデルの番号である。白金の複素誘電率と分散モデルで近似した複素誘電率をFig.2に示す。
| Model1 |
|---|
| Model2 | |||
|---|---|---|---|
| Model3 | |||
| Model4 |
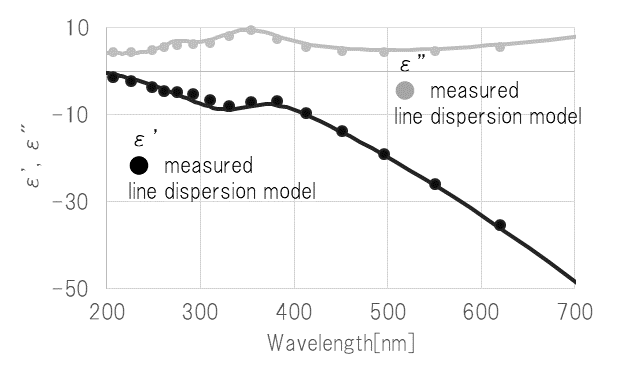 Fig.2 Relative permittivity of platinum
Fig.2 Relative permittivity of platinum
この条件で中心周波数800[THz]のガウシアンパルスを入射し、入射波形と白金ナノ粒子層を透過・反射した波形のフーリエ変換後のエネルギー比から透過・反射スペクトルを算出した。
3. 解析結果
Fig.3に透過・反射スペクトルを示す。透過率は波長570[nm]より短波長側で低下し430[nm]で最小値を示した。反射率は小さく、透過率低下の要因は吸収である。Fig.4に波長430、700[nm]の正弦波を入射した時の粒子近傍電界分布を示す。430[nm]で粒子表面に電界集中が見られ、局在表面プラズモン共鳴(LSPR)による吸収が捉えられている。
 Fig.3 Reflectance and transmittance spectra
Fig.3 Reflectance and transmittance spectra
4. まとめ
分散モデルで近似した白金ナノ粒子の光学特性をFDTD法により導出した。粒径80[nm]ではLSPRにより波長430[nm]で最小値となる可視~紫外域の透過率低下が確認された。
お問い合わせ・資料ダウンロード・入門動画視聴のお申し込みはこちら
お問合せフォームを開く

![波長430[nm]の電界強度分布](https://storage.googleapis.com/kagiken-www-assets/2020/12/Pt_80nm_exp2_sin_430nm_sum-min.png)
![波長700[nm]の電界強度分布](https://storage.googleapis.com/kagiken-www-assets/2020/12/Pt_80nm_exp2_sin_700nm_sum-min.png)