【電磁波解析の基礎用語】

メッシュ生成ー物性値と形状再現

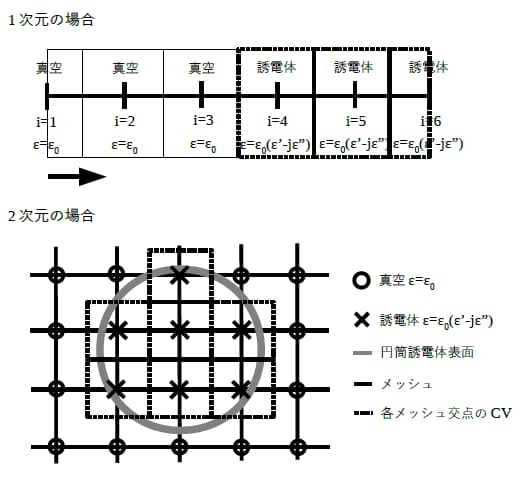
生成は、1.メッシュ分割、2.物性値割当て、という2ステップの手続きです。始めに、解析領域全体を或る有限サイズのメッシュに分割します＜メッシュ分割＞。次に、各メッシュの交点に物性値を割当てます＜物性値割当て＞。励振源及び解析対象もメッシュ分割します。上図は等間隔且つ直交なメッシュで分割し、誘電率を割当てた例です。

1次元の場合メッシュの形状は線分です。解析領域を複数の線分に分割します（i=1~i=2の線分、i=2~i=3の線分、…、i=5~i=6の線分）。そして線分同士の交点に物性値を割当てます(i=1に真空の誘電率、i=2に真空の誘電率、…、i=6に誘電体の誘電率)。コントロールボリューム(CV)の観点で言えば、i=1を中心とした真空のCVがあり、i=2を中心とした真空のCVがあり、…と理解してください。i=3とi=4の中間には真空と誘電体の界面があります。

2次元の場合メッシュの形状は平面です。解析領域を複数の平面に分割し、平面同士の交点に物性値を割当てます(〇の位置に真空の誘電率、×の位置に誘電体の誘電率)。円筒誘電体もメッシュ分割され、点線で示すCVの群で表現されます。凸形状で近似されることが重要です。解析によってはこの解像度では不足する場合もあり得ますし、十分かもしれません。この見極めは解析の目的を念頭に置いて検討する必要があります。

空間の離散化

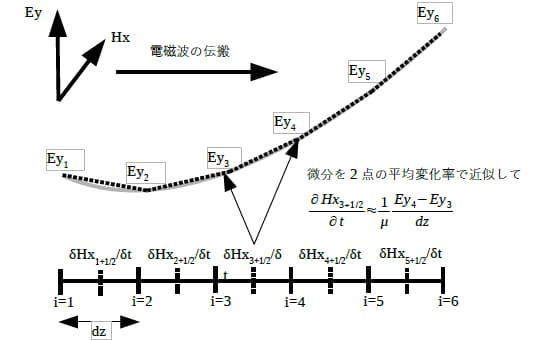
空間の離散化では、電磁波を記述する上で欠かせない電界及び磁界をメッシュに沿って配置していきます。空間微分を含む式を良く見ること、登場する物理量の関係に注意することが重要です。

Z方向の1次元空間を伝搬する電磁波を扱いましょう。Z方向に伝搬する電磁波には「電界成分Ey、磁界成分Hxをもつ電磁波」と「電界成分Ex、磁界成分Hyをもつ電磁波」の2通りが考えられますが、ここでは「電界成分Ey、磁界成分Hxをもつ電磁波」に着目します。

Maxwell方程式の(eq.1-b, eq.1-d)を1次元に適用し、電界Eyと磁界Hxに関する式を求めると次の2式が得られます。(eq.7)から磁界Hxの単位時間の変化はEyの空間微分で求められます。また(eq.8)から電界Eyの単位時間の変化はHxの空間微分で求められます。

差分近似の発想に倣って(eq.7)、(eq.8)を式変形した結果が(eq.9)、(eq.10)です。(eq.9)は、2つ並んだ電界から磁界が計算できることを表します。(eq.10)は、2つ並んだ磁界及び自身の過去の値から電界が計算できることを表します。

電磁波は伝搬するもの、という着想から得られるのが上記の図です。、、、、…と互い違いに配置します。Ey1で励振した電磁波が(eq.9)によってに、更に(eq.10)によってEy2に、そのまた(eq.9)によってに、と伝搬するわけです。FDTD法では電界と磁界を空間・時間的にずらして配置（スタガード配置）して計算を効率的に行います。

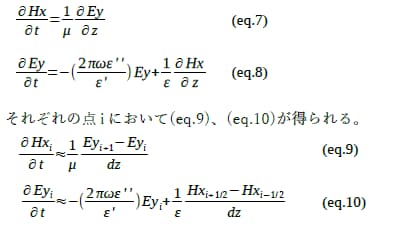
時間の離散化

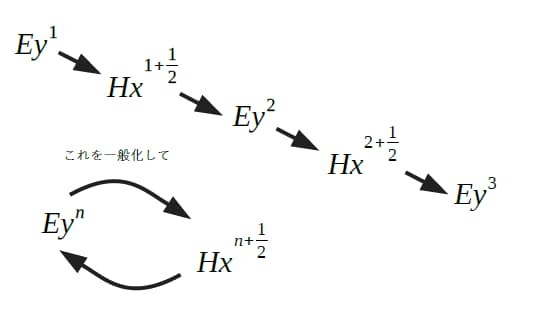
(eq.9), (eq.10)の左辺は電界EyとHxの時間変化を表していますが、これも離散化が必要です。また前述の通り、電界Eyと磁界Hxは時間的にもずらして配置するので電界が時刻n=1, 2, …に存在するとき磁界は時刻n=1+1/2, 2+1/2, …に配置します。

時刻を離散化して時刻n=1と時刻n=2の間隔がとすると左辺を差分化して(eq.11), (eq.12)に書き換えられます。

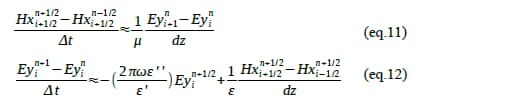
(eq.12)での項が表れていますがこの値をとして、(eq.11)について、(eq.12)についてを求める式に書き換えれば時間についても離散化された式が得られます。

時間を離散化した結果、時間間隔が現れたことに注意して下さい。は一般的にタイムステップと呼ばれシミュレーションでは重要です。

計算時間の考え方

FDTD法ではシミュレーションにかかる時間に関して概ね上の3式で表されることを考慮します。(eq.13)はCFL条件と呼ばれ、タイムステップΔtの間に電磁波がメッシュの間を飛び越えないという条件です。なおこの式の左辺を右辺で割った値はCFL数と呼ばれ、(eq.13)は「CFL数が1以下でなければならない」とも言い換えられます。メッシュ間隔dx, dy, dzが小さくなるとが小さくなることを忘れてはいけません。

FDTD法は物理量を求める際に、過去の情報のみを用いる陽解法なのでCFL数は1以下でなければなりません。物理量を求める際に過去と現在の連立方程式を解く陰解法を用いるFDTD法の場合はCFL数が1以上の場合もありますが、電磁波解析ではこの手法は現段階で一般的ではありません。

(eq.14)は1タイムステップ進めるために必要な解析時間と解析領域の各方向メッシュ数, , の関係を示し、は全メッシュ数()に比例することが分かります。

(eq.15)は解析開始から幅、奥行、高さの解析領域内部に電磁波が行き渡って、定常状態になるまでの解析ステップ数と、、、の関係を示しています。

解析領域を一定として、各方向のメッシュ幅をdx=dy=dz=dhとすると、各方向のメッシュ数はni=W/dh, nj=D/dh, nk=H/dhとなります。またタイムステップはdh/cです。定常解を求めるために必要な全解析時間は1ステップにかかる計算時間(eq.14)とステップ数(eq.15)の積で表され(eq.16)の関係が成り立ちます。

つまり解析領域が同じ大きさでメッシュ幅を各方向均一のメッシュを使用した場合、定常状態を得るための解析時間は「メッシュ幅の4乗に反比例」します。端的に言うとメッシュの密度を2倍にすると定常状態を得るまでの計算時間は16倍になります。

この問題を避けるためには以下の3点について検討が必要です。

計算時間短縮のための3つの検討

• メッシュは3方向で同じ幅である必要はなくX, Y, Z方向でメッシュ数を調整します。但しメッシュ幅が極端に異なると誤差の原因となるためそのアスペクト比は2倍以内に収まるように注意します。
• 少しでもメッシュ幅を大きくします。均一メッシュの場合はメッシュ幅を1.25倍にすると解析時間は40%程度まで短縮できます。
• 不均一メッシュを使用するケースもありますが、誤差の挙動が複雑なので一概には勧めていません。商用ソフトでは解析領域内にメッシュの細かい領域を作るマルチグリッド機能を備えているものがあり、これを使用するほうが有利です。